Advertisements
How Far Quotes
Advertisements
Advertisements
Advertisements
Advertisements
 Friendship Quotes
Friendship Quotes
 Love Quotes
Love Quotes
 Life Quotes
Life Quotes
 Funny Quotes
Funny Quotes
 Motivational Quotes
Motivational Quotes
 Inspirational Quotes
Inspirational Quotes
Advertisements
Text Quotes
How far would I go to be friends with someone? Halfway. (How Far Quotes)
I would far rather feel remorse than know how to define it (How Far Quotes)
Yes,it is remarkable how far a person can travel by sea (How Far Quotes)
Not knowing how near the truth is, we seek it far away (How Far Quotes)
It’s so crazy to look at your life and see how far you’ve come (How Far Quotes)
How far, in any case, must one go back to find the beginning? (How Far Quotes)
Every Journey, no matter how far, starts with one step (How Far Quotes)
I’ll never go. How can I? How far would I get without my heart? (How Far Quotes)
Our fate is determined by how far we are prepared to push ourselves to stay alive - the decisions we make to survive. We must do whatever it takes to endure and make it through alive (How Far Quotes)
How fares it with the happy dead? (How Far Quotes)
It’s not about how far you fall, but how high you rebound (How Far Quotes)
No matter how far a person can go the horizon is still way beyond you (How Far Quotes)
Tact in audacity is knowing how far you can go without going too far (How Far Quotes)
How far have I to go to find you in whom I have already arrived (How Far Quotes)
Take pride in how far you have come. Have faith in how far you can go (How Far Quotes)
I just want to keep acting and better my craft and see how far it goes (How Far Quotes)
The art of genius is knowing how far out is too far (How Far Quotes)
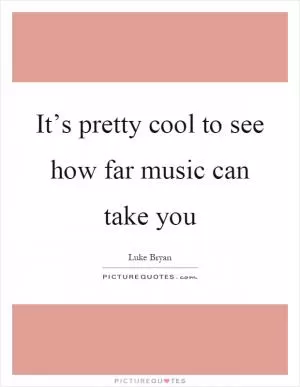
It’s pretty cool to see how far music can take you (How Far Quotes)
Some people said I was annoying, but now look how far we’ve come (How Far Quotes)
The only time you should ever look back is to see how far you've come (How Far Quotes)
Scars remind me of just how far that I’ve come (How Far Quotes)
How far you go in life depends on (How Far Quotes)
You never know how far you can go unless you run (How Far Quotes)
Oh! that gentleness! how far more potent is it than force! (How Far Quotes)
How far should a person go in the name of true love? (How Far Quotes)
No matter how far back you cut a willow tree, it will never really die (How Far Quotes)
No matter how far you travel, you can never get away from yourself (How Far Quotes)
How far would you go to keep the hope of love alive? (How Far Quotes)
It’s not how far you fall, but how high you bounce that counts (How Far Quotes)
Distance might not solve anything, no matter how far you run (How Far Quotes)